Faster Cryptonets: Leveraging Sparsity for Real-World Encrypted Inference

Abstract

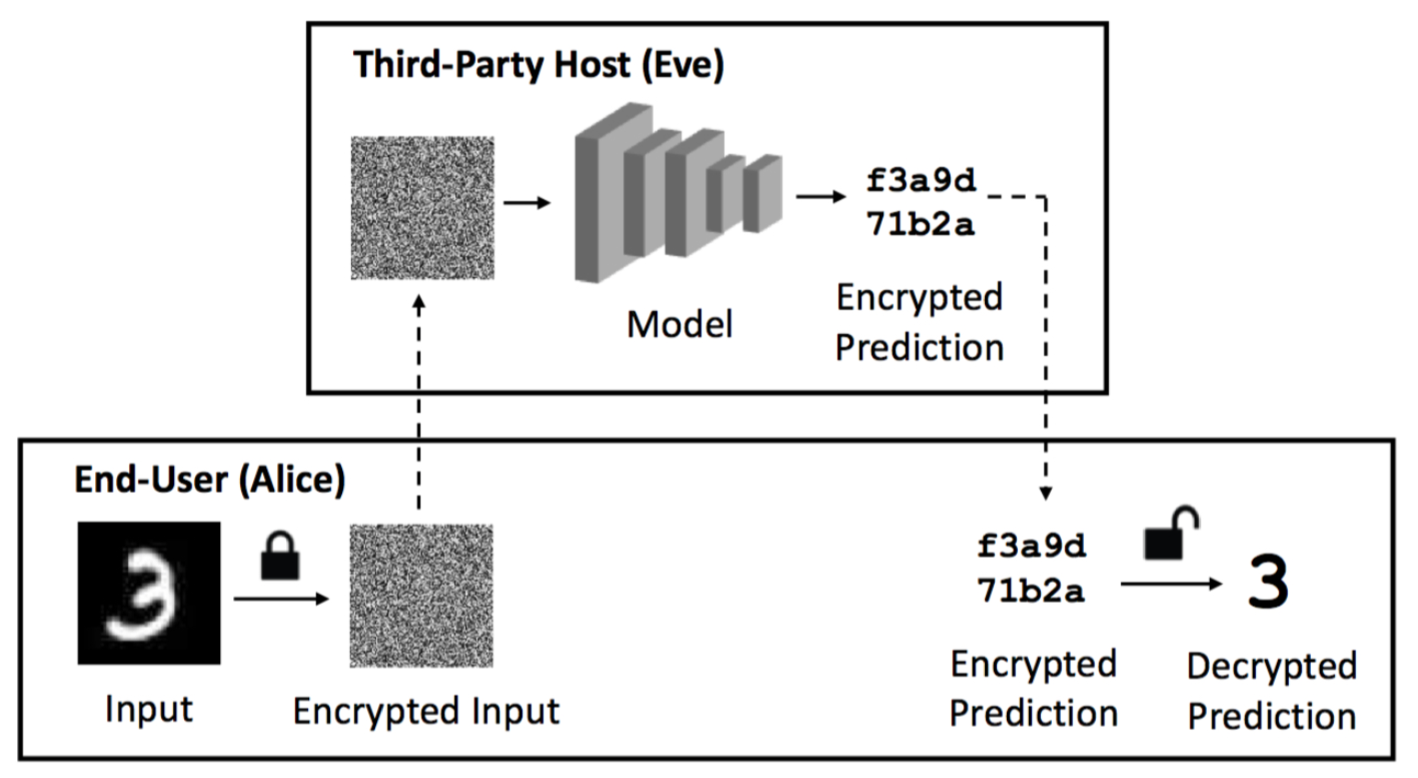
Homomorphic encryption enables arbitrary computation over data while it remains encrypted. This privacy-preserving feature is attractive for machine learning, but requires significant computational time due to the large overhead of the encryption scheme. We present Faster CryptoNets, a method for efficient encrypted inference using neural networks. We develop a pruning and quantization approach that leverages sparse representations in the underlying cryptosystem to accelerate inference. We derive an optimal approximation for popular activation functions that achieves maximally-sparse encodings and minimizes approximation error. We also show how privacy-safe training techniques can be used to reduce the overhead of encrypted inference for real-world datasets by leveraging transfer learning and differential privacy. Our experiments show that our method maintains competitive accuracy and achieves a significant speedup over previous methods. This work increases the viability of deep learning systems that use homomorphic encryption to protect user privacy.